New Book on Discrete Energy Optimizes Hardin-Saff Collaboration
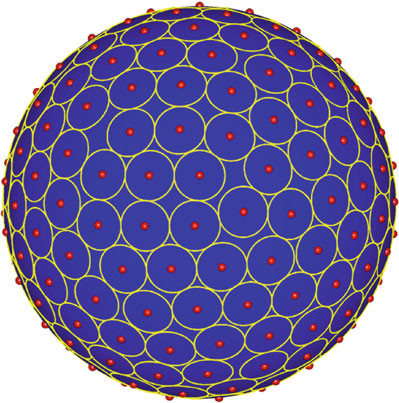A near best-packing of 200 identical spherical caps on S2
Professors Doug Hardin and Ed Saff have published a book that draws on their many years of collaboration in the area of discrete energy and optimal point configurations. Entitled Discrete Energy on Rectifiable Sets, this 670 page opus was co-authored with their former Vanderbilt student Sergiy Borodachov, now a professor at Towson University. It is published in the Springer Monographs in Mathematics series.
The book studies the distribution of point configurations arising from pairwise interactions on manifolds. This topic appears in many contexts of interest to the scientific community, including statistical sampling, quadrature rules, information theory, coding techniques, computer-aided design, interpolation schemes, finite element tessellations, and ground states of matter. The authors focus on minimal energy problems that give rise to point configurations that provide useful discretizations of manifolds.
Comprising 14 chapters, the monograph provides an in-depth examination of the subject. Beginning with basic properties and examples of minimal discrete energy and an introduction to best-packing and best-covering, the authors continue with detailed topics such as continuous energy and its relation to discrete energy, linear programming bounds and universal optimality on the sphere, and optimal discrete measures for potentials (the Chebyshev problem), to name only a few.
Hardin and Saff have worked and published extensively together on the mathematics of particle interactions. In spring 2018 they co-organized a semester program on Point Configurations in Geometry, Physics, and Computer Science at the Institute for Computational and Experimental Research in Mathematics (ICERM) at Brown University, for which Saff served as director. The program involved not only senior researchers but graduate students and post-doctoral fellows for whom mentors and career guidance seminars were provided. The semester included 4 five-day workshops and more than 230 participants.